深入理解CRDT-YATA篇

pedrogao大约 14 分钟

前言

上一篇文章探讨了 RGA 算法的原理与实现，本文我们将介绍另一种 CRDT 算法——YATAopen in new window。

YATA 全称为 Yet Another Transformation Approach，于 2016 年由 Kevin 在论文 Near Real-Time Peer-to-Peer Shared Editing on Extensible Data Typesopen in new window 中提出。

该论文不仅贡献了 YATA 算法，还给出了 YATA 算法的开源 CRDT 协同库——Yjsopen in new window。

Yjs 有着良好的架构设计，运行性能、内存消耗方面都十分优异，而且有着良好的生态，是目前生产环境使用最广泛的 CRDT 算法。

因此 YATA 是学习 CRDT，入门协同的必经之路。

Near Real-Time Peer-to-Peer Shared Editing on Extensible Data Typesopen in new window论文详细阐述了协同算法的发展历史，尤其是介绍部分基本囊括了所有主流的协同算法，是学习协同算法的必读论文。

YATA

三条规则

YATA 认为文档是插入操作的集合，保证文档有序的关键是保证插入操作有序，因此 YATA 的核心是插入操作——o：

o_k(id_k, origin_k, left_k, right_k, isDeleted_k, content_k),

$id_k$ ：操作的唯一标识，由 lamport 时钟实现，即[siteId, clock]；
$origin_k$ ：操作意图，操作创建时，左边相邻的操作项 $o_i$ ，不会改变；
$left_k$ ： $o_k$ 左边操作项；
$right_k$ ： $o_k$ 右边操作项；
$isDeleted_k$ ：操作是否被删除；
$content_k$ ：插入的内容。

插入操作抽象为 $o$ ，删除时，将 $o$ 的 $isDeleted$ 置为true； $left$ 与 $right$ 是操作之间的左、右链接，构建出完整的插入有序链表。

遍历整个有序链表，筛掉被删除的操作，即可得到有序的文档内容。

$origin$ 的存在是为了解决并发插入问题，如下图所示：

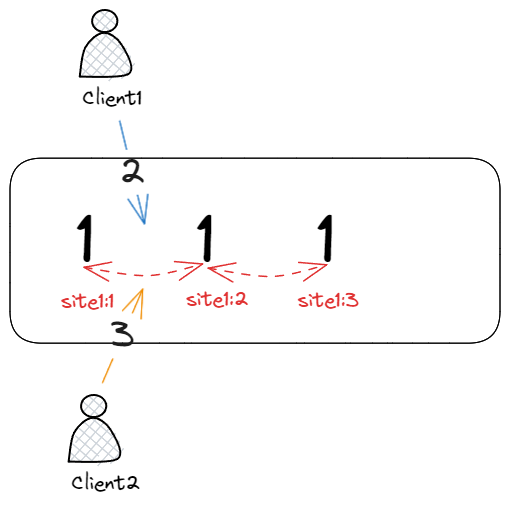
yata1

客户端 1、2 同时在文本111中的同一位置插入新的字符2，3，此时客户端 1、2 的操作都是并发的，因此无法确定谁先谁后，对于这类并发冲突 YATA 定义了 3 条规则：

禁止origin连线交叉；
插入操作必须严格按照顺序排列，如果 $o_1$ 与 $o_2$ 相邻，且 $o_1$ 在左边，即满足 $o_1 <_c o_2$ ，那么不可能找到另外一个 $o_i$ 比 $o_1$ 大，同时比 $o_2$ 小，即不可能存在 $o_1 <_c o_i <_c o_2$ ；
如果两个插入操作的origin一致，那么 id 大的字符在右边；

规则 2 很好理解，插入操作必须严格按照顺序排列，否则无法保证文档的有序性。

规则 3 借鉴了 OT 算法，当两个操作的origin一致时，由于无法通过origin来比较顺序，因此按照id来比较，由于id是唯一且确定的，这样可以保证文档在任何客户端都能最终收敛到一致。

这里，笔者尝试用自己的理解来解释规则 1，首先，origin连线是这样的：

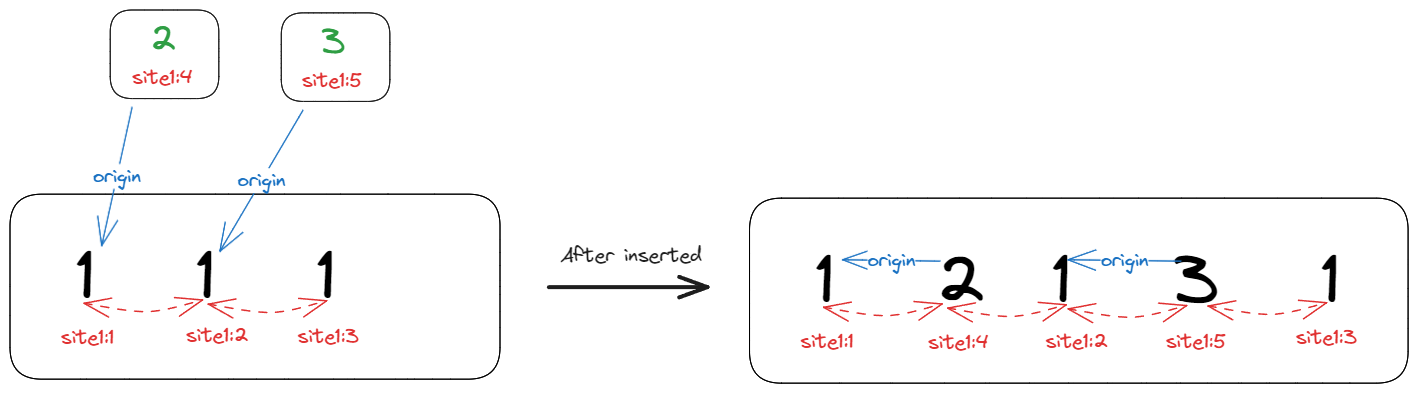
yata2

字符插入后，左右连线指向当前相邻的字符，而origin连线只会一直指向操作创建时的左边字符，并且不会改变。

origin连接不会交叉，即不会出现这样的情况：

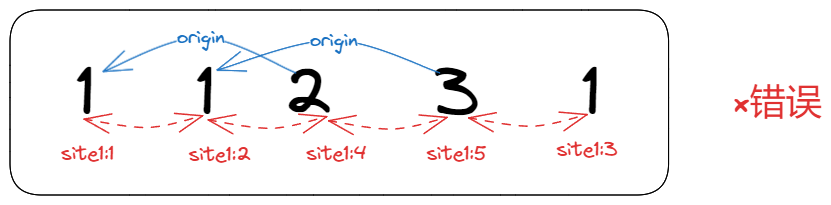
yata3

而下面的两种情况是允许的：

yata4

通过规则 1，操作意图origin与操作o这样就能得到如下的性质：

o_1 <_{rule1} o_2 ⇔ o_1 < origin_2 ∨ origin_2 ≤ origin_1

操作 $o_1$ 如果在操作 $o_2$ 的左边，通过规则 1，就能推导得出下面两种 case：

case1， $o_1$ 在 $origin_2$ 的左边，即 $o_1 < origin_2$ ；
case2， $origin_2$ 在 $origin_1$ 的左边，或者 $origin_2$ 与 $origin_1$ 是同一个操作，即 $origin_2 ≤ origin_1$ 。

有了 rule1，2，3，YATA 就能保证只要操作意图origin不变，那么插入操作在任意副本都能收敛到全局有序，即文档内容是一致的。

规则 1 不好理解，论文其实并没有给出为什么要引入规则 1，而是给出规则 1,2,3 后，通过严格的数学公式证明所有插入操作最终有序；当然这也足够了，明确前提条件，能够推理正确就算理解 YATA 了；对推理过程感兴趣的可以直接看论文open in new window。

插入算法

每次插入操作都需要满足上面的 3 条规则，如果不满足，就需要调整操作的位置，使其满足规则。这样就能得出插入算法：

yata5

insert函数有两个参数：

i：插入操作，即 $o_k(id_k, origin_k, left_k, right_k, isDeleted_k, content_k)$ ；
ops：与i有冲突的插入操作列表；

函数作用是将i插入到ops中，使其满足规则 1，2，3。

函数虽然只有 10 行左右的代码，但理解起来不容易，下面笔者尝试用自己的理解来解释这个函数。

将插入操作 $i$ 插入到ops中，实际是在寻找 $i.left$ —— $o$ ，然后将 $i$ 插入到 $o$ 后面，即 $o < i$ 。

$o < i$ 需要满足上面的 3 条规则（ $o_r$ ： $o$ 的 $origin$ ； $i_r$ ： $i$ 的 $origin$ ）：

如果 $o_r < i_r < o < i$ ，那么origin存在交叉，无法满足，直接 break，对应算法中的breaking condition；

如果 $i_r < o_r < o < i$ ，或者 $o_r < o < i_r < i$ ，满足规则 1；

如果 $o_r = i_r < o < i$ ，需比较 creator，满足规则 3；

满足规则 1,3，那么 $i.position + 1$ ，直至找到满足规则 2 的 $o$ 为止，对应图中的for range。

YATA 算法虽然推理起来很麻烦，但实际上最后的算法代码很少，对应到 Yjs 实现上也就是几十行代码open in new window而已。

案例

介绍完 YATA 原理后，可以体验一下 YATA 的实际案例open in new window，如下是一个纯文本编辑器：

Network

Latency

100

只支持简单的英文、数字文本增、删，不支持中文、复制粘贴等操作。
没办法，input 中文事件笔者不会啊。

在左侧输入框中编辑文本内容，都会同步到对方，最终保证两个输入框的内容一致。

实现

在理解 YATA 算法的基础上，我们再来看看 YATA 的实现open in new window。

YATA 版

首先，抽象出 YATA 的插入操作：

export type Item<T> = {
  content: T;
  id: Id;
  isDeleted: boolean;
  origin: Id | null; // null if insert at doc's begin
};

Item包含了content、id、isDeleted、origin四个属性，分别对应 YATA 插入操作的 $content_k$ 、 $id_k$ 、 $isDeleted_k$ 、 $origin_k$ 。

再看看文档的数据结构：

export class Doc<T> {
  content: Item<T>[];
  length: number;
  vector: Vector;
  clientId: string;

  public constructor(clientId?: string) {
    const cid = clientId ?? randomString(6);
    this.content = [];
    this.length = 0;
    this.vector = {};
    this.clientId = cid;
  }
}

Item中之所有没有 $left_k$ 、 $right_k$ ，是因为这里的实现没有选择双向链表，而是统一存储在Doc中的content列表。

content：文档内容，即Item列表；
length：文档长度，筛掉删除的Item后的列表长度；
vector：clock 向量；
clientId：客户端 ID；

首先看看insert函数：

  public insert(pos: number, content: T) {
    const clock = this.vector[this.clientId] ?? -1;
    // origin is previous item of pos
    const i = this.findPositionByIndex(pos);
    // create current item of pos
    const item: Item<T> = {
      content,
      id: [this.clientId, clock + 1],
      isDeleted: false,
      origin: this.content[i - 1]?.id ?? null,
    };

    this.integrate(item);
  }

因为墓碑机制的存在，所以pos并不是content的下标，而是content中未删除的Item的下标，所以需要先通过findPositionByIndex函数找到pos对应的Item的下标i。

然后，创建Item，并调用integrate函数将其插入到content中，注意：origin是创建时的左侧Item节点。

整个insert的核心是integrate，对应 YATA 中插入解决冲突部分：

  private integrate(item: Item<T>) {
    const lastClock = this.vector[item.id[0]] ?? -1;
    const clock = item.id[1];
    if (lastClock + 1 !== clock) {
      throw new Error("Clock not match");
    }
    this.vector[item.id[0]] = clock;

    // origin always front of the item
    // the origin.right may be conflict with the item
    // find the right place for the item start with origin.right
    let origin = this.findItemById(item.origin);
    let destIndex = origin + 1;
    let scanning = false;

    // search o, which i is successor of o
    // ir < or < o < i
    // or < o < ir < i
    // or = ir < minClient(o, i) < maxClient(o, i)

    // The logic below can be summarized in these two lines:
    // if (oleft < left || (oleft === left && newItem.id[0] <= o.id[0])) break
    // if (oleft === left) scanning = newItem.id[0] <= o.id[0]
    for (let i = destIndex; ; i++) {
      if (!scanning) {
        destIndex = i;
      }
      if (i === this.content.length) {
        break;
      }

      const o = this.content[i];
      const oorigin = this.findItemById(item.origin);
      // Insert i before o
      // case1: or < ir < i < o => break
      // case2: or = ir < min(i, o) < max(i, o) => break
      if (oorigin < origin || (oorigin === origin && item.id[0] <= o.id[0])) {
        break;
      }
      if (oorigin === origin) {
        scanning = item.id[0] <= o.id[0];
      }
    }

    if (!item.isDeleted) {
      this.length += 1;
    }
    this.content.splice(destIndex, 0, item);
  }

首先，检查clock是否连续，如果不连续则抛出异常；
然后，根据origin找到初始目标下标destIndex，即item的插入位置，因为并发冲突都是在origin后发生的，因此destIndex的初始值为origin的下标加 1；
判断出o与item之间是否满足 3 条规则，满足则后移，直至找到item的插入位置，不满足则跳出循环，即已找到插入位置；
最后，将item插入到content中。

delete函数十分简单，找到pos对应item然后标记isDeleted即可：

  public delete(pos: number) {
    const i = this.findPositionByIndex(pos);
    const item = this.content[i];
    if (!item) {
      throw new Error("Item not found");
    }
    item.isDeleted = true;
    this.length -= 1;
  }

Yjs 优化版

YATA 版实现了论文原有的插入算法，但这版插入算法其实有一个严重的 base case：

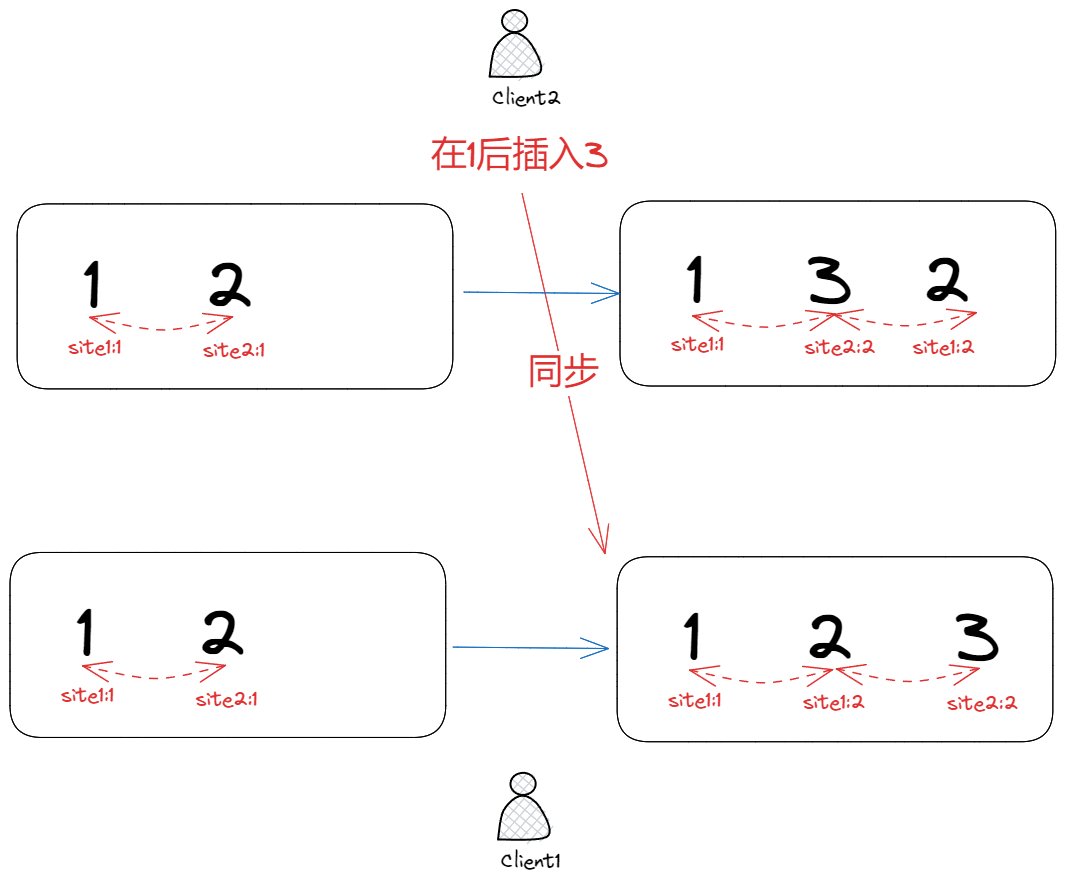
yata6

客户端 1，2 有同一段文本12，1是2的origin，现在客户端 2 向1插入了一个3，按照算法规则，文本会变成132；

可一旦操作同步到客户端 1，因为字符3的origin是1，且3的id大，因此会跑到2的后面，导致文本变成123，这就导致了双方最终内容不一致。

为了解决这个问题，yjs 引入了另外一个属性originRight，同时规定插入的操作排序后必须在originRight之前，这样客户端 2 插入3时，由于originRight是2，因此3会插入到2的前面，最终文本变成132，双方达成一致，这样就解决了这个问题。

有了originRight后，插入操作 $o$ 就变成了这样：

o_k(id_k, origin_k, originRight_k, left_k, right_k, isDeleted_k, content_k),

而这一版的实现open in new window，抽象出了新的Item类：

export type Item<T> = {
  content: T;
  id: Id;
  isDeleted: boolean;

  originLeft: Id | null; // null if insert at doc's begin
  originRight: Id | null; // null if insert at doc's end
};

originLeft：对应上面的origin；
originRight：即 yjs 新增的originRight；

Doc定义不变，而insert函数有了些许变化：

  public insert(pos: number, content: T) {
    const clock = this.vector[this.clientId] ?? -1;
    // origin is previous item of pos
    const i = this.findPositionByIndex(pos);
    // create current item of pos
    const item: Item<T> = {
      content,
      id: [this.clientId, clock + 1],
      isDeleted: false,
      originLeft: this.content[i - 1]?.id ?? null,
      originRight: this.content[i]?.id ?? null,
    };
    this.integrate(item);
  }

item在新建时，需要同时指定originLeft和originRight，且后面不会再变化。另外 integrate 也增加了originRight的判断条件：

private integrate(item: Item<T>) {
    const lastClock = this.vector[item.id[0]] ?? -1;
    const clock = item.id[1];
    if (lastClock + 1 !== clock) {
      throw new Error("Clock not match");
    }
    this.vector[item.id[0]] = clock;
    let left = this.findItemById(item.originLeft);
    let right = this.findItemById(item.originRight);
    let destIndex = left + 1;
    let scanning = false;

    for (let i = destIndex; ; i++) {
      if (!scanning) {
        destIndex = i;
      }
      if (i === this.content.length) {
        break;
      }
      // 1. Must insert between originLeft and originRight
      if (i === right) {
        break;
      }

      const o = this.content[i];
      const oleft = this.findItemById(item.originLeft);
      const oright = this.findItemById(item.originRight); // 2.
      if (
        oleft < left ||
        (oleft === left && oright == right && item.id[0] <= o.id[0]) // 3.
      ) {
        break;
      }
      if (oleft === left) {
        scanning = item.id[0] <= o.id[0];
      }
    }

    if (!item.isDeleted) {
      this.length += 1;
    }
    this.content.splice(destIndex, 0, item);
  }

上面的注释 1、2、3 处增加了originRight的判断，即必须在originLeft和originRight之间，这样就保证了插入的顺序。

TinyYjs

yjs 是目前生产环境使用最为广泛 CRDT 库，其设计思想和实现优化都非常值得学习。

TinyYjsopen in new window 是笔者实现的一个精简版 yjs，支持YMap，YArray，YText（纯文本，不支持富文本）三种数据类型，实现了基本的 CRDT 功能，但没有实现 yjs 的优化，因此可以作为一个学习 yjs 的入门项目。

YArray：
- insert(index, content)
- get(index): any
- delete(index)
- toArray(): any[]
YText：
- insert(index, content)
- get(index): any
- delete(index)
- toString(): string
YMap：
- set(key, value)
- get(key): any
- delete(key)
- has(key): boolean
- toJSON(): any

下面分别就这 3 个基础类型来介绍 TinyYjs 的实现。

数据建模

在 tinyyjs 中，每个插入操作被抽象为Item：

export class Item {
  content: ContentAny;
  id: Id;
  isDeleted: boolean;

  originLeft: Id | null; // null if insert at doc's begin
  originRight: Id | null; // null if insert at doc's end

  left: Item | null;
  right: Item | null;

  parent: AbstractType | null;
  parentSub: string | null;

  public constructor(
    content: ContentAny,
    id: Id,
    isDeleted: boolean,
    originLeft: Id | null,
    originRight: Id | null,
    left: Item | null,
    right: Item | null,
    parent: AbstractType | null,
    parentSub: string | null
  ) {
    this.content = content;
    this.id = id;
    this.isDeleted = isDeleted;
    this.originLeft = originLeft;
    this.originRight = originRight;
    this.left = left;
    this.right = right;
    this.parent = parent;
    this.parentSub = parentSub;
  }
}

export class Doc {
  share: Map<string, AbstractType>;
  vector: Vector;
  clientId: string;
  store: Map<string, Item[]>; // client id => item list

  public constructor(clientId?: string) {
    const cid = clientId ?? randomString(6);
    this.share = new Map();
    this.vector = {};
    this.clientId = cid;
    this.store = new Map();
  }
}

content，id，isDeleted，originLeft，originRight 与上面保持一致；
left，right是链表的左右指针，分别指向前后两个操作；

Doc.share是一个Map，key 是AbstractType的名字，value 是AbstractType的实例。

Item.parent 指向父节点AbstractType；AbstractType是 YArray，YMap，YText 等数据类型的基类，一个Item属于一个AbstractType，这样Doc就能支持多数据类型。如下：

  public getText(name: string = ""): YText {
    if (!this.share.has(name)) {
      const at = new YText(this);
      this.share.set(name, at);
    }
    return this.share.get(name) as YText;
  }

  public getArray(name: string = ""): YArray {
    if (!this.share.has(name)) {
      const at = new YArray(this);
      this.share.set(name, at);
    }
    return this.share.get(name) as YArray;
  }

如果Item的 parent 为空，代表该Item是游离节点，会被垃圾回收掉。

对于 YArray，YText 这类线性数据结构而言，Item之间通过连续的双向链表连接在一起，如下图：

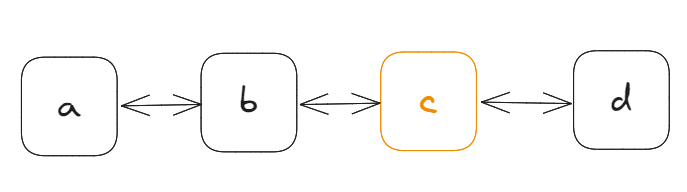
yata7

对于 YMap 而言，Item之间是分离的，如下图：

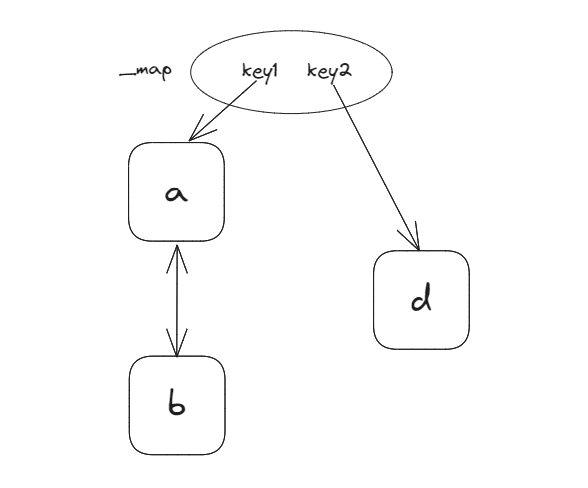
yata8

Item.parentSub用来表示YMap的 key，Item是YMap的 value，一个key上的value可能会被多个客户端操作，因此value是一个小双向链表。

遵循LWW(Last Write Won)规则，最后写入的Item会覆盖之前写入的Item，上图中key1下有两个Item，而生效的是a。

Doc.share中所有的AbstractType实例，其Item都会被存储在Doc.store中，key 是clientId，value 是Item数组。

冲突解决

数据建模是 tinyyjs 参考 yjs 简化而来，并以此支持多数据类型，由于是多种数据类型，因此冲突解决需要稍加改变一下：

  public integrate(doc: Doc) {
    const parent: AbstractType = this.parent!;
    const parentSub = this.parentSub;
    const getItem = (id: Id | null) => doc.getItem(id);
    if (
      (!this.left && (!this.right || this.right.left !== null)) ||
      (this.left && this.left.right !== this.right)
    ) {
      let left = this.left; // 插入时的左边节点，即插入origin

      let o; // 是否具有冲突的节点
      // set o to the first conflicting item
      if (left !== null) {
        // list, text set left to the first conflicting item
        o = left.right;
      } else if (parentSub !== null) {
        // map sets left to the first item with the same key
        o = parent._map.get(parentSub) || null;
        while (o !== null && o.left !== null) {
          // map, set o to the first item of key
          o = o.left;
        }
      } else {
        o = parent._start; // default set o to the first item
      }

      const conflictingItems = new Set();
      const itemsBeforeOrigin = new Set();
      // Let c in conflictingItems, b in itemsBeforeOrigin
      // ***{origin}bbbb{this}{c,b}{c,b}{o}***
      // Note that conflictingItems is a subset of itemsBeforeOrigin
      while (o !== null && o !== this.right) {
        itemsBeforeOrigin.add(o);
        conflictingItems.add(o);
        if (Id.compare(this.originLeft, o.originLeft)) {
          // case 1
          if (o.id[0] < this.id[0]) {
            // 如果o的clientID小于this的clientID，那么o在this的左边，大的在右边
            left = o;
            conflictingItems.clear();
          } else if (Id.compare(this.originRight, o.originRight)) {
            // 右插入意图相同，则直接break
            // this and o are conflicting and point to the same integration points. The id decides which item comes first.
            // Since this is to the left of o, we can break here
            break;
          } // else, o might be integrated before an item that this conflicts with. If so, we will find it in the next iterations
        } else if (
          o.originLeft !== null &&
          itemsBeforeOrigin.has(getItem(o.originLeft))
        ) {
          // use getItem instead of getItemCleanEnd because we don't want / need to split items.
          // case 2
          if (!conflictingItems.has(getItem(o.originLeft))) {
            left = o;
            conflictingItems.clear();
          }
        } else {
          break; // 直接break，会发生意图交叉
        }
        o = o.right;
      }
      this.left = left;
    }
    // reconnect left/right + update parent map/start if necessary
    if (this.left !== null) {
      const right = this.left.right;
      this.right = right;
      this.left.right = this;
    } else {
      let r;
      if (parentSub !== null) {
        r = parent._map.get(parentSub) || null;
        while (r !== null && r.left !== null) {
          r = r.left;
        }
      } else {
        r = parent._start;
        parent._start = this;
      }
      this.right = r;
    }
    // for map
    if (this.right !== null) {
      this.right.left = this;
    } else if (parentSub !== null) {
      // set as current parent value if right === null and this is parentSub
      parent._map.set(parentSub, this);
      if (this.left !== null) {
        // this is the current attribute value of parent. delete right
        this.left.delete();
      }
    }
    doc.addItem(this);
  }

这段冲突解决代码几乎与 yjsopen in new window 一致，这里简单解释一下。

Item插入时，Item.left会被初始化为Item.originLeft，因此与其有冲突的节点从Item.left开始，直到Item.right，这些节点都有可能是冲突节点。
如果是 YArray，YText，第一个冲突节点是left.right，如果是 YMap，第一个冲突节点是parent._map.get(parentSub)对应的最左边节点；
插入位置需要遵循 3 条规则，虽然改成了双向链表，但是判断逻辑基本一致；
最后，将Item插入到链表中。

对于 tinyyjs 的介绍就到这里，感兴趣的可以查看源码open in new window。

结语

关于 YATA 算法，就介绍到这里。

后续文章会对 yjs 实现做一次解密，看看明星 CRDT 库是如何实现的。

深入理解CRDT-YATA篇

# 前言

# YATA

# 三条规则

# 插入算法

# 案例

# 实现

# YATA 版

# Yjs 优化版

# TinyYjs

# 数据建模

# 冲突解决

# 结语

# 参考资料

前言