深入理解CRDT-RGA篇

pedrogao大约 14 分钟

前言

上一篇文章我们介绍了 CRDT 的基本概念，探讨了一些基础 CRDT 的实现。从本篇文章开始，我们将深入两种 CRDT 算法：

这两种算法分别是知名 CRDT 库 Automerge 和 Yjs 所采用的算法，被广泛应用于生产环境，是深入 CRDT 应用的基础。

本篇文章我们将介绍 RGA 算法，下一篇文章我们将介绍 YATA 算法。

RGA

RGA 全称 Replicate Growable Array 可复制增长数组，由 Hyun 于 2011 年在论文Replicated abstract data types: Building blocks for collaborative applicationsopen in new window中提出（2011 年真的是 CRDT 爆发的一年）。

千万别被名字吓到了，其实 RGA 就是列表的 CRDT 实现。论文原话是：
growable array is the Vector class of JAVA or STL.

论文中提到 RGA 在有序复制集合上拥有良好的插入、删除性能，优于已有的 OT 算法，适合用于协同文本编辑场景。

当然 RGA 不仅适用于有序文本，同时也能推广到有序列表，哈希表等场景，因此 RGA 也是 Automerge 库的基础。

论文中，给出了 RGA 基于双向链表实现的部分伪代码，如下：

RGA-local-operations

伪代码实现十分简单，无论是插入还是删除，都是在链表中排除已删除项，找到i对应的位置，然后插入或删除即可。

不过，双向链表显然无法满足大文本编辑、查找等场景的性能要求，因此有不少优化版的 RGA 实现，比如：

Automergeopen in new window 中 RGA 是基于 B+树实现的；
Colaopen in new window中 RGA 是基于 G-tree 实现的；
RGATreeSplitopen in new window使用平衡树来优化 RGA；

案例

下面，以纯文本协同编辑open in new window为例，看看 RGA 是如何工作的。

Network

Latency

100

只支持简单的英文、数字文本增、删，不支持中文、复制粘贴等操作。
没办法，input 中文事件笔者不会啊。

在左侧输入框中编辑文本内容，都会同步到对方，最终保证两个输入框的内容一致。

推演

文本内容本质上是插入操作的集合，因此我们可以通过插入操作来推演 RGA 的工作原理。

下面，以纯文本协同编辑为例，看看 RGA 是保证多方编辑内容最终一致的。

首先，我们看一个最简单的例子：有且只有一个客户端进行编辑

rga1

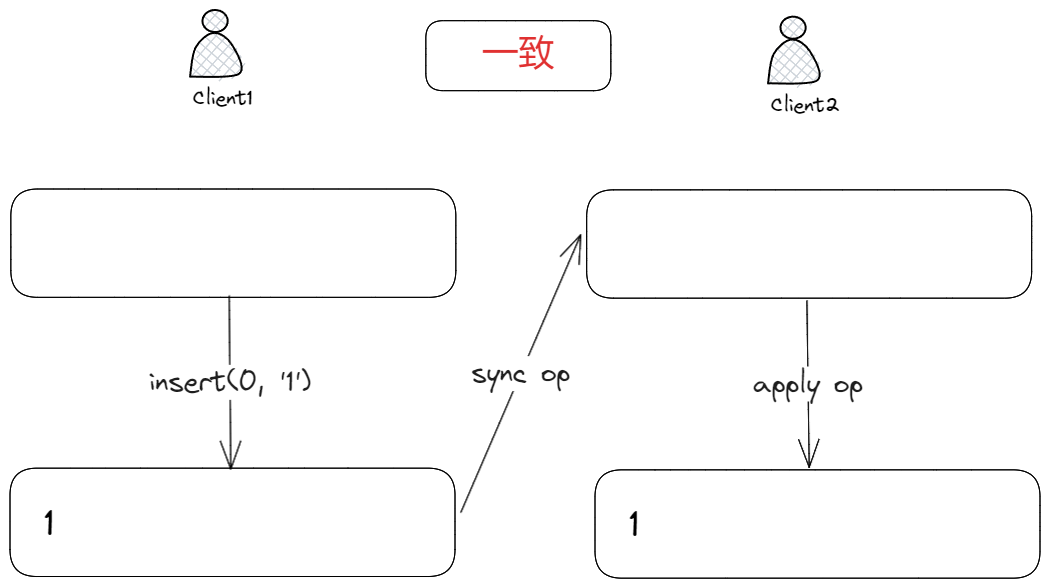
客户端 1 在位置0插入字符1，并将插入操作(op)同步到客户端 2，客户端 2 收到 op 并应用后，将1插入到位置0，此时客户端 1 和客户端 2 的文本内容是一致的。

因为只有客户端 1 有编辑操作，其它客户端处于只读状态，那么就不能产生编辑冲突，因此最后的文本内容肯定是一致的。

可一旦有多个客户端同时进行编辑，就会产生编辑冲突，导致最终文本内容不一致，比如：

rga2

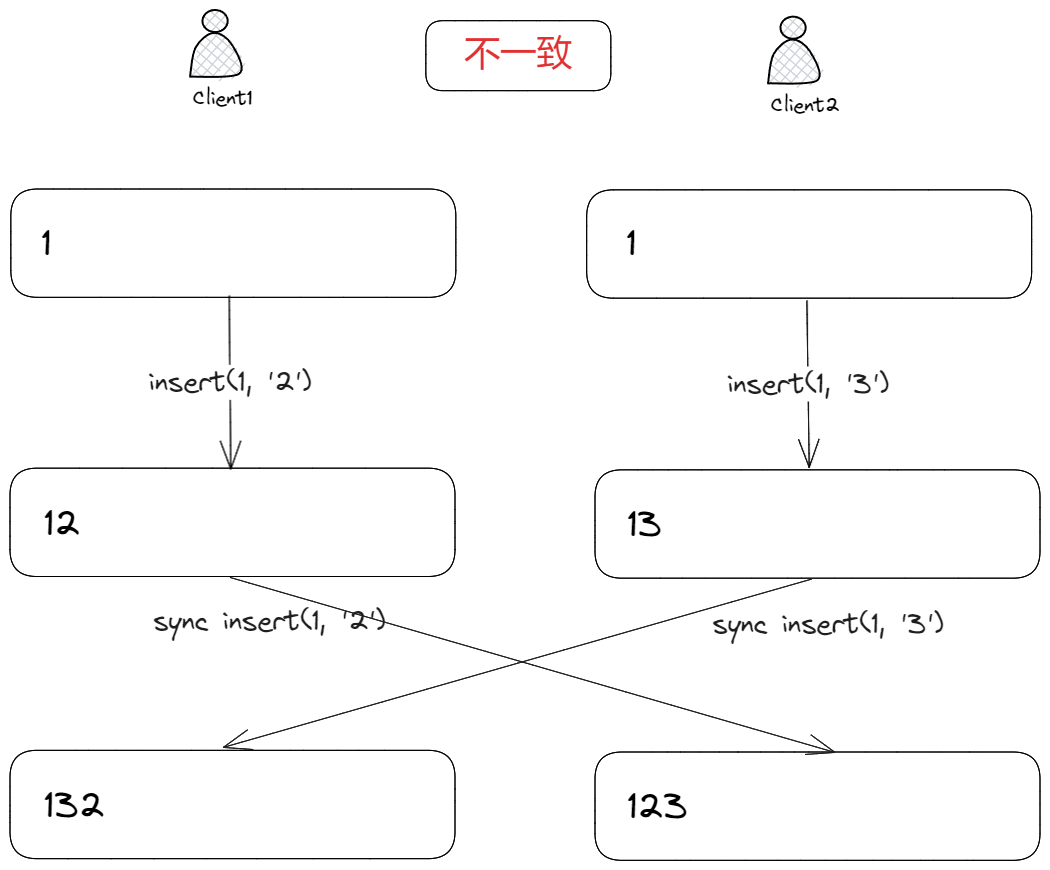
客户端 1、2 分别在位置1插入字符2、3，并将插入操作(op)同步到对方应用后，此时客户端 1 和客户端 2 的文本内容不一致。

而产生不一致的原因是，操作同步的数据：

insert(1, "2");

虽然携带了插入位置1和插入数据2，但没有其它约束条件，导致最终文本内容不一致。

我们可以通过插入意图来解决这个问题：

client1: insert(1, "2", "1");
client2: insert(1, "3", "1");

这里，"1"就是插入意图，表示在1之后插入2，3，但这样就能保证最终文本内容一致吗？

显然是不能的，因为1虽然是插入意图，但是文本中可能存在多个1，比如：

rga3

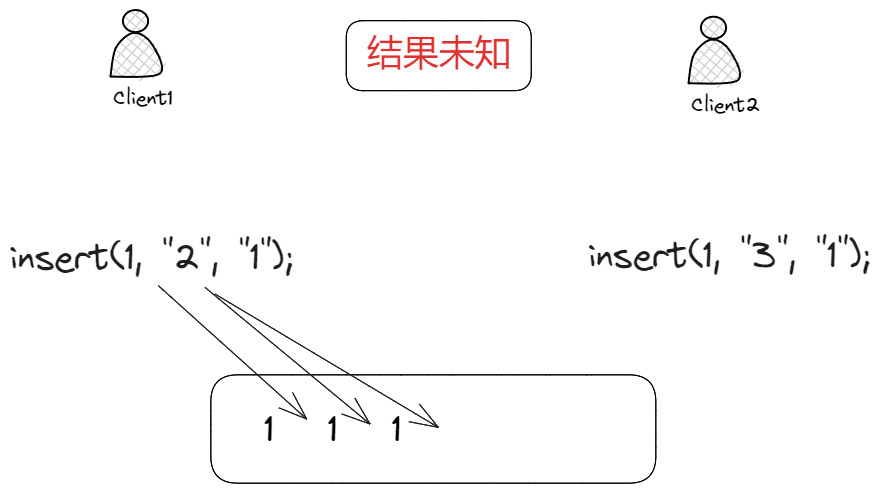
我们为每个插入字符都添加一个唯一的标识符 Id，比如字符1的 Id：

// [siteId, counter]
export type Id = [string, number];

Id 包括两部分，第一部分是客户端的唯一标识符，第二部分是客户端操作的序号，这样就能保证每个字符都有唯一的 Id。

有了 Id 后，操作同步数据就变成了：

// params:
// 1. 插入位置
// 2. 插入数据
// 3. 插入意图，即当前插入位置字符的 Id
insert(1, "2", ["site1", 1]);

这样能够保证最终文本内容一致了吗？如下：

rga4

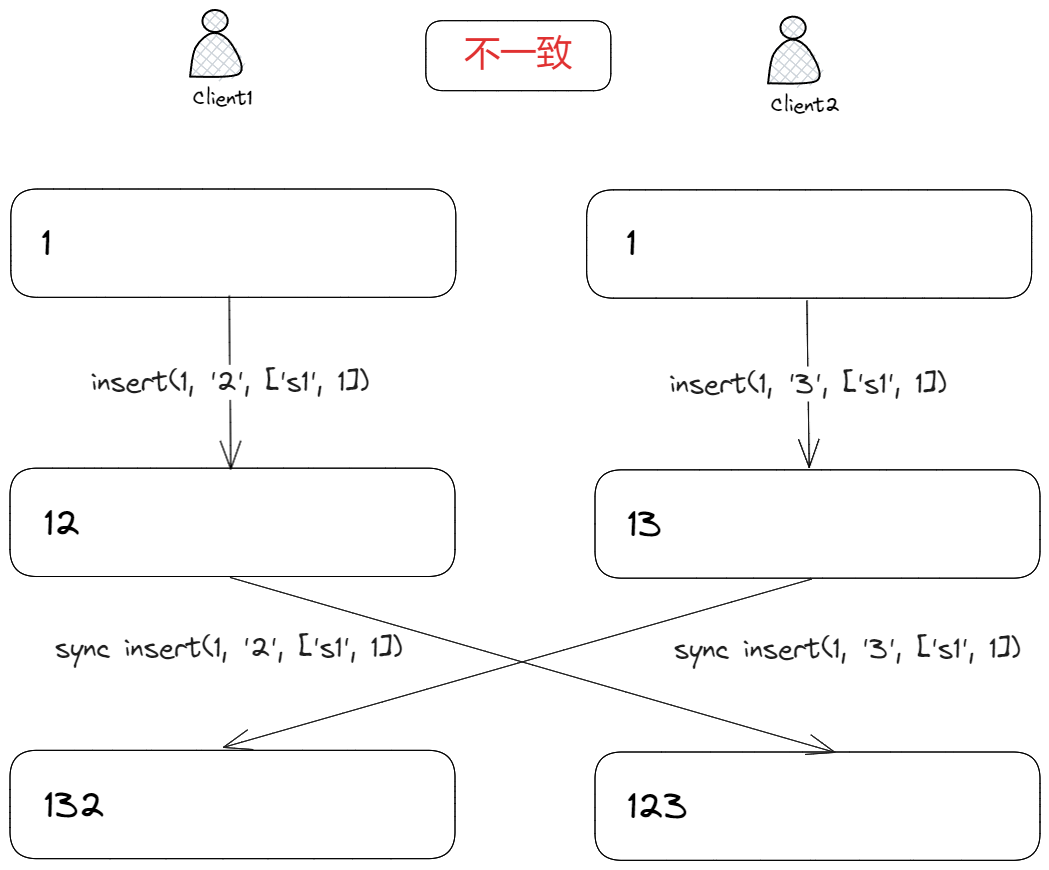
客户端 1、2 分别在位置1插入字符2、3，因为两个插入操作的意图是一致的，都插入在字符1右侧，但字符2，3之间位置暂时不知如何排列，从而导致最终文本内容不一致。

我们可以通过字符2，3的 Id 来解决二者之间的插入排序问题，即：

client1: insert(1, { id: ["site1", 2], content: "2" }, ["site1", 1]);
client2: insert(1, { id: ["site2", 1], content: "3" }, ["site1", 1]);

约定，如果插入意图一致，那么就按照字符 Id 来排序：

如果counter不同，那么按照counter排序，大者在右边；
如果counter相同，那么按照siteId排序，大者在右边；

有了排序后，最终文本内容就一致了：

rga5

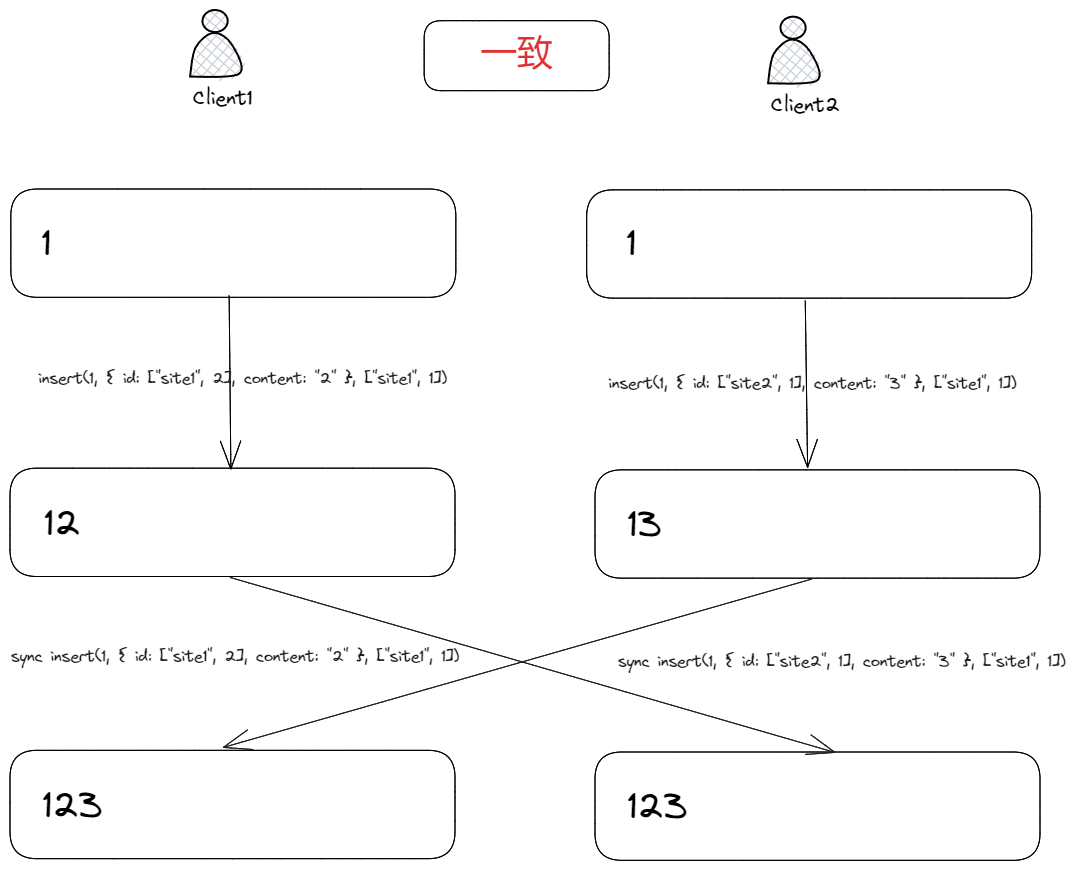
最后，来看看删除操作，我们将一次插入抽象为一个Item，即：

export type Item<T> = {
  content: T | null; // 插入内容
  id: Id; // Id
  parent: Id | null; // 插入意图
};

至于删除，最容易想到的是将Item直接删除掉，但这显然不行，因此不同客户端可能在同一个插入意图上工作，如果将字符删除掉了，那么意图也就丢失了，文本最终内容也就不一致了。

因此，我们不能直接删除Item，而是引入墓碑机制，即：

export type Item<T> = {
  content: T | null; // 插入内容
  id: Id; // Id
  isDeleted: boolean;
  parent: Id | null; // 插入意图
};

删除Item时，将isDeleted设置为 true，这样就能保留插入意图，从而保证最终文本内容一致。

实现

充分推演后，我们就能给出一个简单 RGA 的实现open in new window了。

首先是数据建模，每个插入字符操作被抽象为一个Item：

export type Item<T> = {
  content: T | null; // root item has no content
  id: Id;
  isDeleted: boolean;
  children: Id[]; // children of this item
  parent: Id | null; // parent of this item
};

parent：插入意图；
children：子节点，每个字符都可能成为多个字符的意图，因此子节点可能有多个；

很明显，这样的数据结构导致文本内容是一个树：

rga6

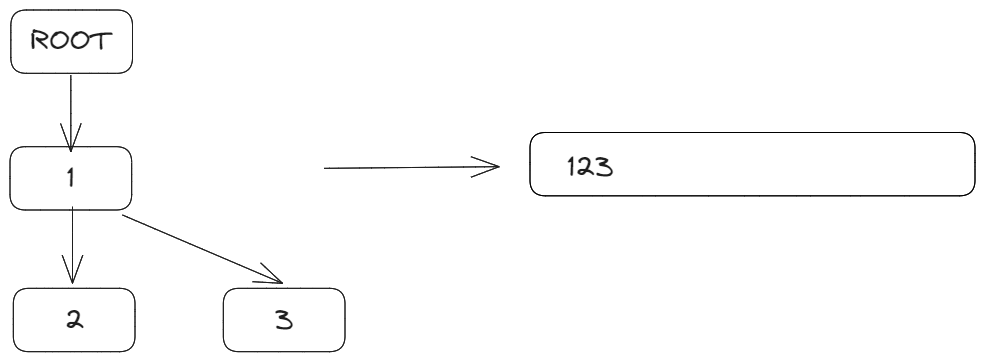
ROOT 节点是虚拟节点，标识文档的开始，没有实际意义。

因此我们可以使用Map来存储Item，其中key是Item.id，value是Item。

export class Doc<T> {
  root: Id;
  length: number;
  vector: Vector;
  clientId: string;
  store: Map<string, Item<T>>;

  public constructor(clientId?: string) {
    const cid = clientId ?? randomString(6);
    const root = {
      content: null,
      id: [cid, 0],
      isDeleted: false,
      children: [],
      parent: null,
    } as Item<T>;

    // Root item should insert at the beginning, and could not be deleted or updated
    this.root = root.id;
    this.length = 0; // Exclude root item
    this.vector = {
      [cid]: 0,
    };
    this.clientId = cid;
    this.store = new Map([[Id.hash(root.id), root]]);
  }
}

root：文档的根节点，虚拟节点；
length：文档长度，不包括根节点；
vector：客户端向量；
clientId：客户端唯一标识符；
store：存储Item的Map；

新建Doc时，向store中插入根节点，同时设置length、vector。

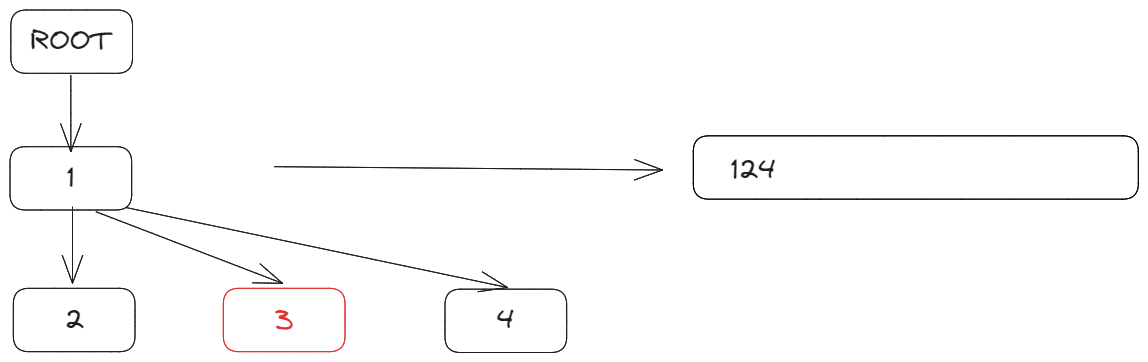
由于整个文档是一颗树，每个字符是其中一个节点，获取文档内容时，我们需要遍历整个树，将所有字符拼接起来：

rga7

  public getContent(): T[] {
    const doc = this;
    const content: T[] = [];
    const queue: Id[] = [];

    queue.push(doc.root);
    while (queue.length > 0) {
      const id = queue.shift()!;
      const item = doc.store.get(Id.hash(id))!;
      if (!item.isDeleted && item.content !== null) {
        content.push(item.content);
      }
      queue.push(...item.children);
    }

    return content;
  }

由于字符3被软删除掉了，因此最终文本内容是[1, 2, 4]。

接下来是插入操作，插入操作的核心是生成Item，然后将集成(intergrate，下文再详谈)到文档树中。

  public insert(pos: number, content: T) {
    const item = this.findItemByIndex(pos - 1);
    if (!item) {
      throw new Error("Item not found");
    }

    const newItem = {
      content,
      id: [this.clientId, this.vector[this.clientId] + 1],
      isDeleted: false,
      children: [],
      parent: item.id,
    } as Item<T>;

    this.integrate(newItem);
  }

insert将字符插入到pos位置，因此需要找到pos-1位置的Item作为其插入意图 parent，然后生成新的Item，最后将其集成到文档树中。

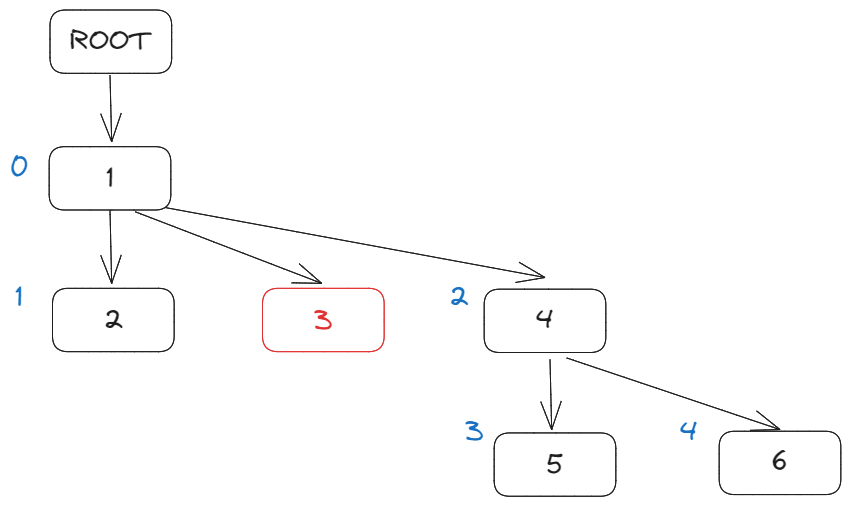
findItemByIndex使用 DFS 遍历文档树，排除掉删除字符，找到pos位置的Item：

rga8

  private findItemByIndex(pos: number): Item<T> | null {
    if (pos === -1) {
      return this.store.get(Id.hash(this.root))!;
    }

    const queue: Id[] = [];
    let i = pos;
    // DFS
    queue.push(this.root);
    while (queue.length > 0) {
      const id = queue.shift()!;
      const item = this.store.get(Id.hash(id))!;
      if (item.content === null) {
        queue.push(...item.children);
        continue;
      }

      if (i === 0 && !item.isDeleted) {
        return item;
      }

      if (!item.isDeleted) {
        i--;
      }
      queue.push(...item.children);
    }

    return null;
  }

有了findItemByIndex有，删除就十分简单了：

  public delete(pos: number) {
    const item = this.findItemByIndex(pos);
    if (!item) {
      throw new Error("Item not found");
    }
    item.isDeleted = true;
    this.length -= 1;
  }

最后，解释一下最复杂的integrate：

private integrate(item: Item<T>) {
    const lastClock = this.vector[item.id[0]] ?? 0;
    const clock = item.id[1];
    if (lastClock >= clock) {
      // This item has been integrated
      return;
    }
    if (lastClock + 1 !== clock) {
      throw new Error("Clock not match");
    }
    this.vector[item.id[0]] = clock;
    // 1. Find the parent item
    // 2. Insert the new item to parent.children, compare the id of new item and the next item
    // 3. Update the version and length of doc
    const parent =
      item.parent![1] === 0
        ? this.store.get(Id.hash(this.root))!
        : this.store.get(Id.hash(item.parent!))!;
    if (!parent) {
      // Root item can not integrate
      throw new Error("Parent not found");
    }

    let destIndex = 0;
    for (; destIndex < parent.children.length; destIndex++) {
      const child = parent.children[destIndex];
      // Smaller id should at left
      if (item.id[0] <= child[0]) {
        break;
      }
    }

    parent.children.splice(destIndex, 0, item.id);
    this.store.set(Id.hash(item.id), item);
    if (!item.isDeleted && item.content !== null) {
      this.length += 1;
    }
  }

integrate 有三个核心步骤：

clock去重逻辑，如果item已经被集成到文档树中，那么就不需要再次集成了；
找到item的parent，然后将item插入到parent.children中，这里需要注意的是，item的id需要和parent.children中的id进行比较，保证id小的在左边，大的在右边；
更新doc的length和vector；

TinyAutomerge

Automerge 是为数不多将 RGA 用在生产环境上的 CRDT 库，RGA 是 Automerge 中的核心算法部分，设计方式和实现思路都很有借鉴性。

笔者实现了一个 toy 版本：TinyAutomergeopen in new window。

TinyAutomerge 是 Automerge 的一个极简版本，它是按照笔者个人理解以及 Automerge 文档open in new window来实现的，可以帮助我们更好的理解 Automerge 和 RGA。

Automerge 中 RGA 的实现文档open in new window其实已经被官方文档删除掉了，笔者在 github 上找到了以前的 commit，然后将其复制到了飞书文档，希望能帮助到对 Automerge 感兴趣的人

TinyAutomerge 支持两种 CRDT 数据类型以及其基本操作：

List(Text):
- insert(pos, content)
- delete(pos)
- put(pos, content)
- get(pos)
- range(start, end)
Map:
- put(key, value)
- get(key)
- delete(key)
- range(start, end)

Text 纯文本本质上和 List 是一样的，因此这里没有额外实现。

下面就 Automerge 核心数据结构建模以及基本操作伪代码做一个简单的介绍。

数据结构建模

TinyAutomerge仍然以Operation(操作)作为核心建模方式，任何一个基本操作，包括insert、delete、put、get都可以被抽象为一个Operation：

export type Operation<T> = {
  id: OpId;
  prop: string; // map property name or array insert|update origin intention
  insert: boolean;
  value: T | null | "make(map)" | "make(list)"; // null means delete
  pred: OpId[];
  succ: OpId[];
};

这里的OpId其实也是 Lamport 时钟，也即是[actorId, clock]，actorId是一个字符串，clock是一个数字。

在Automerge中 actorId 其实就是siteId。

每个Operation都有唯一的id，insert字段表示是否为插入操作；

prop字段略微有点特殊，对于Map来说，prop就是map中的某个key，对于List来说，prop 操作意图，即插入位置前一项。

另外 pred 和 succ 字段分别标识操作的前驱、后继操作，以Map为例，如果多个put操作的key相同，那么这些put操作的pred和succ就会形成一个双链表，最后的操作在链表最后端。

如果Operation的 succ 不为空，证明这个Operation已经过期了，因为有新的Operation插入到了这个Operation之后。

而delete略有不同，因为 delete 没有实际的删除数据，只是将上一个Operation的succ指向自己，这样就可以将Operation从链表中软移除了。

同样地，文档是操作的集合：

type OpTree<T> = {
  parent: ObjId | null; // null means root
  objType: ObjType; // map or list
  store: Array<Operation<T>>; // sorted by OpId or Prop
};

type OpSet<T> = {
  // Op trees
  trees: Map<ObjId, OpTree<T>>;
  // The length of op array
  length: number;
};

export type Doc<T> = {
  ops: OpSet<T>;
  // The current actor.
  id: Actor;
  // The maximum operation counter this document has seen.
  maxOpCount: number;
};

Doc核心数据实际就是op的集合，即OpSet。OpSet 下可以有多个 OpTree，每个 OpTree 对应一个Map或者List，OpTree 中的store是一个操作有序数组，parent指向父节点，objType标识是Map还是List。

从这里就可以得出，对于Map和List的操作一般需要两步：

在OpSet中找到对应的OpTree，如果没有就创建一个；
在OpTree中查找、变更、对应的Operation；

Map

了解了基本数据结构后，我们就可以来看看Map的基本操作实现了。

get

伪代码：

def get(store, prop):
    operations, _ := search(store, prop);
    last := operations[opertaions.len - 1];
    return last.value;

def search(store, prop):
    result := [];
    start_idx := index of the first row that matches prop
    end_idx := store.length
    for i in range(start_idx, end_idx):
        if store[i].prop != prop:
            return result, i;
        result.append(store[i]);
    return result, end_idx + 1;

get(prop)：

查找store，找到与prop相关的所有Operation；
返回最后一个Operation的value；

put

伪代码：

def put(store, prop, value):
    operations, last_idx := search(store, prop)
    last := operations[opertaions.len - 1];
    pred := [last.id]

    local_op := {
        op: lamport_clock_inc(),
        obj: table.objId,
        prop,
        value: "{value}",
        pred,
        succ: []
    }
    last.succ.append(local_op.id);
    insert_op(store, local_op, last_idx);

put(prop, value)：

查找store，找到与prop相关的所有Operation；
生成一个新的Operation，pred指向最后一个Operation；
将最后一个Operation的succ指向新的Operation；
将新的Operation插入到store中；

delete

伪代码：

def delete(store, prop):
    operations, _ := search(store, prop)
    last := operations[opertaions.len - 1];
    pred := [last.id]

    new_clock := lamport_clock_inc()
    last.succ.append(new_clock);

delete(prop)：

查找store，找到与prop之相关的所有Operation；
生成新的 lamport_clock，加入到最后一个Operation的succ中；

delete 不会生成新的Operation，而是将最后一个Operation的succ指向新的lamport_clock，这样就可以将Operation从链表中软移除了。如下：

rga9

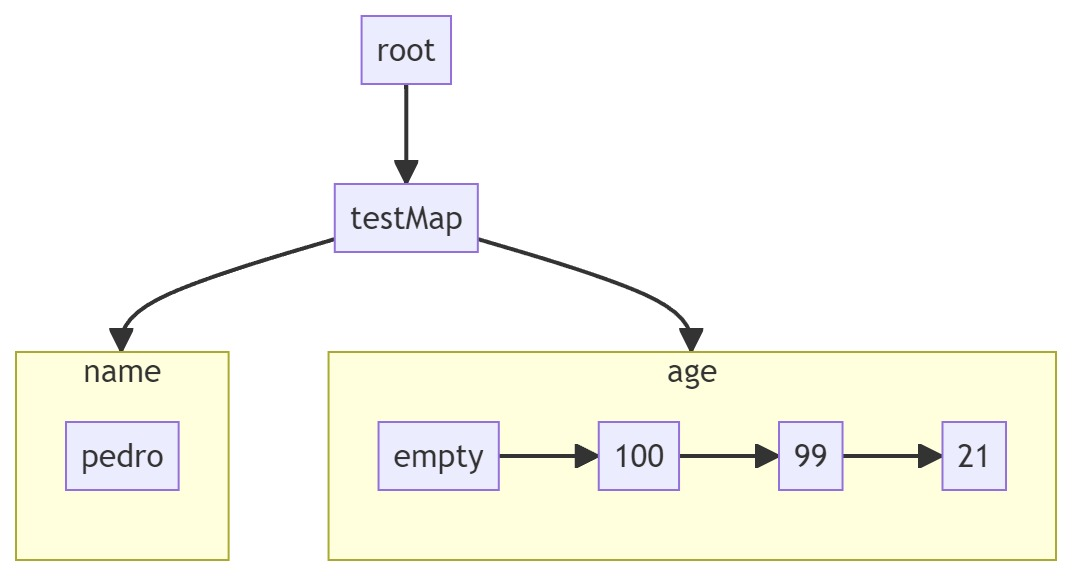
empty表示空的Operation，只有一个lamport lock并指向age最后一个Operation 100，从而达到删除age的效果。

List

List的实现稍微复杂一点，因为List没有明确的key，而index也是动态变化的，所以找到会更加麻烦一点。

get

伪代码：

def get(store, index):
    operations, _ := nth(store, index);
    last := operations[operations.len - 1];
    return last.action.value;

def nth(store, index):
    seen = 0;
    // current position
    pos := 0;
    // result operations
    res = [];

    for operation in store:
        if operation is insert:
            if seen > index:
                return res, pos;

        if operation.insert && operation.succ.length == 0:
                seen += 1;

        if seen == index && operation.succ.length == 0:
            res.append(operation);

        pos++;

    return res, pos;

get(index)：

核心点在nth即找到第index个Item上，注意不是Operation。一个列表Item会包括一个或者多个Operation。

遍历store，找到第index个Item；
返回最后一个Operation的value；

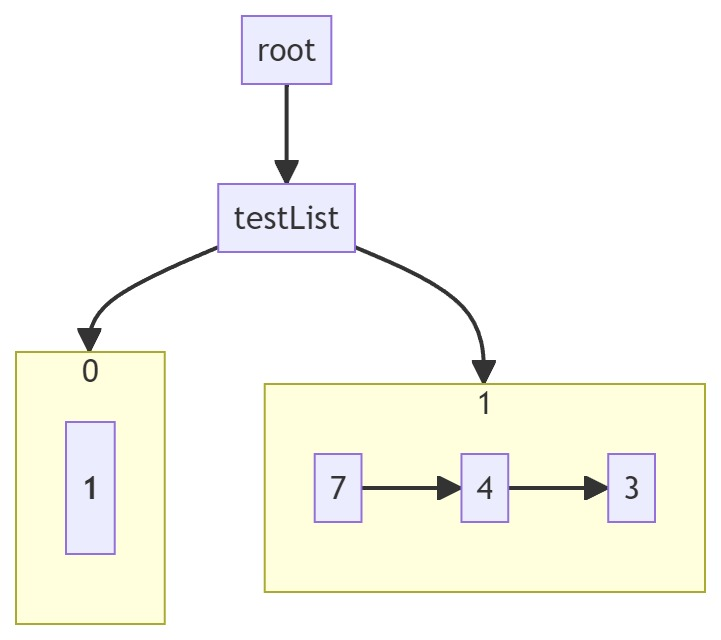
rga11

如上图所示，第0项 Item 只有 1 个Operation，第1项 Item 有 3 个Operation。

delete

伪代码：

def delete(store, index):
    operations, _ := nth(store, index);
    first := operations[0];
    new_clock := lamport_clock_inc()
    first.succ.append(new_clock);

delete(index)：

遍历store，找到第index个Item，即operations；
生成新的 lamport_clock，加入到第一个Operation的succ中；

这里与 Map 不同，Map 的delete是在最后一个Operation上加入新的lamport_clock，而 List 是在第一个Operation上加入新的lamport_clock。

insert

伪代码：

def insert(store, index, value):
    operations, idx := nth(store, index);
    firstOp = operations[0];
    prop = firstOp ? (firstOp.insert ? firstOp.id : firstOp.prop) : obj;
    pred = firstOp ? [firstOp.id] : [];
    local_op := {
            op: lamport_clock_inc(),
            obj: store.id,
            prop,
            action: "{value}",
            succ: null,
            pred,
    };
    if firstOp:
        firstOp.pred.append(local_op.id);
    insert_op(store, local_op, idx);

insert(index, value)：

遍历store，找到第index个Item；
生成一个新的Operation，pred指向firstOp，firstOp 可能为空，即插入一个新的Item；
将firstOp的pred指向新的Operation；
将新的Operation插入到store中；

put

伪代码：

def put(store, index, value):
    operations, idx := nth(store, index);
    if operations.len == 0:
        return; # not found
    firstOp = operations[0];
    prop = firstOp.id;
    pred = firstOp ? [firstOp.id] : [];
    local_op := {
            op: lamport_clock_inc(),
            obj: store.id,
            prop,
            action: "{value}",
            succ: null,
            pred,
    };
    firstOp.pred.append(local_op.id);
    insert_op(store, local_op, idx);

put(index, value)基本与insert类似，但 put 不能插入新的Item，只能修改已有的Item。

因此未找到Item时，直接返回；而prop实际就是firstOp.id，第一个插入Operation的 id。

对于Text，其实本质与List大差不差，只是value是一个字符而已，当然如果需要支持富文本，那就没那么简单了。

RGA 富文本实现可参考peritextopen in new window。

结语

本文以 RGA 为切入点，介绍了其基本原理和实现，并参考 RGA 在 Automerge 中的设计，给出了 TinyAutomerge 的实现。

希望能够帮助读者对 CRDT 与 RGA 有一个更加深入的理解。

深入理解CRDT-RGA篇

# 前言

# RGA

# 案例

# 推演

# 实现

# TinyAutomerge

# 数据结构建模

# Map

# get

# put

# delete

# List

# get

# delete

# insert

# put

# 结语

# 参考资料

前言

RGA

案例

推演

实现

TinyAutomerge

数据结构建模

Map

get

put

delete

List

get

delete

insert

put

结语

参考资料