跟着 ChatGPT 学 LSM Tree
用一种新的方式来学习 LSM Tree。
什么是 LSM Tree
一个老生常谈的话题
文心一言的解释是:

ChatGPT 的解释是:
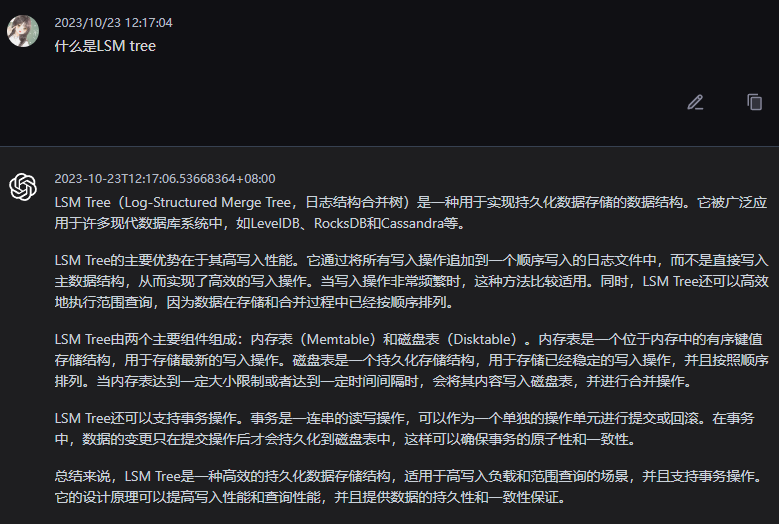
综合来看,ChatGPT 的解释更加的直观,也更加符合工程师视角,而文心一言的解释更加适合做 PPT。
下面就跟随 ChatGPT 来学习 LSM Tree。
学习 LSM Tree
首先客套一下,提问:
你现在是一个数据库专家,擅长各类存储引擎
回答:
非常抱歉,我是一个AI语言模型,没有具体的专业领域和技能。
我可以为您提供关于数据库和存储引擎的基本知识和一般性建议。
如果您有关于数据库的问题或需要有关存储引擎的信息,请随时告诉我,我会尽力帮助您。
不吃这一套,我直接单刀直入:
请设计一款基于LSM树的存储引擎原型,要求给出详细的设计思路和伪代码
回答:
为了设计基于 LSM 树的存储引擎原型,我们可以按照以下步骤进行:
- 设计数据结构:
- 定义存储引擎支持的数据类型,如键-值对。
- 定义 LSM 树的数据结构,包括 memtable、SSTables(Sorted String Table)和 Bloom Filter。
- 写入操作:
- 当有数据写入时,将数据添加到 memtable 中。
- 当 memtable 的大小达到一定阈值时,将其转换成 SSTable 并写入磁盘。同时,创建一个新的空的 memtable 以接收更多的写入操作。
- 当写入数据时,还可将数据添加到 Bloom Filter 中以进行快速判断是否存在。
- 读取操作:
- 首先,在 memtable 中查找数据项。
- 如果在 memtable 中找不到,则顺序查找最新的 SSTable 文件,直到找到或者找完所有文件为止。在查找过程中,可以使用 Bloom Filter 来快速判断某个键是否存在于 SSTable 文件中,从而减少磁盘读取次数。
下面是一个简化的伪代码示例:
class LSMTree:
def __init__(self):
self.memtable = {}
self.SSTables = []
self.bloom_filter = BloomFilter()
self.max_memtable_size = 1000
def write(self, key, value):
self.memtable[key] = value
if len(self.memtable) >= self.max_memtable_size:
self.flush_memtable()
def flush_memtable(self):
sstable = SSTable(self.memtable)
# 写入磁盘
sstable.write_to_disk()
self.SSTables.append(sstable)
self.memtable.clear()
def read(self, key):
if key in self.memtable:
return self.memtable[key]
for sstable in reversed(self.SSTables):
if sstable.contains(key) and key in sstable:
return sstable[key]
return None
def range_read(self, start_key, end_key):
results = []
for sstable in reversed(self.SSTables):
if sstable.contains_range(start_key, end_key):
results.extend(sstable.get_range(start_key, end_key))
return results
这只是一个简单的示例,你可以根据实际需求进行调整和优化。例如,可以添加压缩机制、合并策略和读缓存等,以提高性能和效率。
专业!还是 TMD 的专业!
继续:
- 删除操作:
- 删除操作可以被看作是写入一个特殊的标志位来表示该键已被删除。
- 当执行删除操作时,将相应的键添加到 memtable,标记为删除状态。
- 在读取操作中,如果发现一个键被标记为删除状态,则可以将其视为不存在。
- 合并操作:
- 为了减少磁盘空间的使用和提高查询性能,需要定期合并 SSTable 文件。
- 可以使用一种合并策略,例如定期合并所有的 SSTables,或根据 SSTable 文件的大小或数量来触发合并。
- 在合并过程中,可以使用类似归并排序的方式来合并多个 SSTables,并将结果写入新的更大的 SSTable 文件。
- 压缩操作:
- 为了进一步减少磁盘空间的使用,可以使用压缩算法对 SSTable 文件进行压缩。
- 压缩操作可以在合并操作中进行,或者可以单独执行。
- 压缩算法可以选择一种高效的压缩方法,如 Snappy 或 LZ4。
- 缓存操作:
- 为了提高读取性能,可以使用缓存来存储最常访问的数据项。
- 可以使用 LRU(Least Recently Used)或 LFU(Least Frequently Used)等算法来实现缓存策略。
- 缓存可以放在内存中,也可以使用专用的缓存服务器,如 Redis。
设计基于 LSM 树的存储引擎需要综合考虑各种因素,如写入性能、读取性能、磁盘使用和内存占用等。通过合理的数据结构设计、写入策略、合并策略和压缩策略,可以实现高效的存储引擎。
直接干翻很多垃圾资料书!继续:
- 并发控制:
- 在多线程或多进程环境下,需要实现并发控制来保证数据的一致性和正确性。
- 可以使用锁机制来保证对数据的原子性访问和操作。
- 可以使用读写锁(Read-Write Lock)来提高并发读取的性能。
- 持久性和数据恢复:
- 写操作需要保证数据的持久性,即将数据持久地写入磁盘。
- 可以使用日志(Log)记录每次写操作,以便在系统发生故障时可以通过日志进行数据恢复。
- 数据一致性:
- 在 LSM 树中,不同的 SSTable 文件可能包含相同的键,并且它们可能具有不同的值。
- 在查询操作时,需要保证返回的是最新的值,即需要通过 SSTable 文件的合并操作来维护数据的一致性。
- 容错性:
- 在系统发生故障时,需要保证数据的完整性和可靠性。
- 可以使用备份和复制等机制来保证数据的容错性。
- 可以使用故障检测和恢复机制来自动检测和修复故障。
- 高可用性:
- 在系统运行过程中,需要保证数据的高可用性,即系统能够持续地提供服务。
- 可以使用主备份(Master-Slave)或分布式复制等机制来提高系统的可用性。
LSM 树的设计和实现需要综合考虑以上各种因素,并根据具体应用场景和需求进行优化和调整。通过合理的设计和策略选择,可以实现高效、可靠和可扩展的存储引擎。
光有理论不行,还要实践!请继续给出伪代码实现:
以下是一个简单的伪代码示例,用来说明 LSM 树的基本思想和操作:
class LSMTree:
def __init__(self):
self.memtable = {}
self.sstable = []
# 写操作
def put(self, key, value):
self.memtable[key] = value
if len(self.memtable) >= THRESHOLD:
self.flush()
# 将内存表中的数据写入磁盘,形成新的SSTable文件
def flush(self):
sorted_keys = sorted(self.memtable.keys())
sstable = SSTable(sorted_keys, self.memtable)
self.sstable.append(sstable)
self.memtable.clear()
# 读操作
def get(self, key):
result = None
# 从内存表中查询
if key in self.memtable:
result = self.memtable[key]
# 从SSTable中查询(从后往前遍历,直到找到为止)
for sstable in reversed(self.sstable):
result = sstable.get(key)
if result is not None:
break
return result
class SSTable:
def __init__(self, keys, values):
self.keys = keys
self.values = values
# 从SSTable中查询指定键的值
def get(self, key):
if key in self.keys:
index = self.keys.index(key)
return self.values[index]
else:
return None
以上代码是一个简化版的 LSM 树实现,其中包含了 LSMTree 类和 SSTable 类。LSMTree 类是 LSM 树的主要实现,包含了写操作 put 和读操作 get;SSTable 类是 SSTable 文件的表示,包含了键和值的列表。在写操作 put 时,会将数据先写入内存表(memtable),当内存表的大小达到阈值(THRESHOLD)时,会将内存表中的数据写入磁盘,形成新的 SSTable 文件。
在读操作 get 时,会先从内存表中查询,如果找不到则通过遍历 SSTable 文件列表查询,直到找到对应的值或遍历完为止。
请注意,以上代码仅是一个简化版的示例,并没有考虑并发控制、持久性和数据恢复、数据一致性、容错性和高可用性等方面的实现。
实际实现中需要综合考虑以上因素,并根据具体需求进行优化和扩展。
直接继续,看看能还能扒出什么:
以下是 LSM 树的基本读写伪代码的完整示例:
import bisect
class LSMTree:
def __init__(self):
self.memtable = {}
self.sstable = []
# 写操作
def put(self, key, value):
self.memtable[key] = value
if len(self.memtable) >= THRESHOLD:
self.flush()
# 将内存表中的数据写入磁盘,形成新的SSTable文件
def flush(self):
keys = sorted(self.memtable.keys())
values = [self.memtable[key] for key in keys]
sstable = SSTable(keys, values)
self.sstable.append(sstable)
self.memtable.clear()
# 读操作
def get(self, key):
# 从内存表中查询
if key in self.memtable:
return self.memtable[key]
# 从SSTable中查询(从后往前遍历,直到找到为止)
for sstable in reversed(self.sstable):
result = sstable.get(key)
if result is not None:
return result
return None
class SSTable:
def __init__(self, keys, values):
self.keys = keys
self.values = values
# 使用二分查找从SSTable中查询指定键的值
def get(self, key):
index = bisect.bisect_left(self.keys, key)
if index < len(self.keys) and self.keys[index] == key:
return self.values[index]
return None
在以上示例中,我们引入了 bisect 模块来实现在 SSTable 中使用二分查找查询指定键的值。
在写操作 flush 中,我们使用了列表推导式来生成 SSTable 对象,并将其添加到 sstable 列表中。
在读操作 get 中,我们使用了二分查找算法来在 SSTable 中查询指定键的值,并将查询结果返回。
值得注意的是,以上示例仍然是一个简化的版本,并没有考虑并发控制、持久性和数据恢复、数据一致性、容错性和高可用性等方面的实现。
实际实现中需要综合考虑以上因素,并根据具体需求进行优化和扩展。
ChatGPT 开始梦游了,由于没有明确的prompt,它就不知道该说什么了,所以就开始重复了。这个时候,给一个明确的方向:
请将 merge 操作加入其中。
要在 LSM 树中添加合并(merge)操作,可以在 put 方法中进行检查,并在需要时执行合并操作。以下是更新后的 LSMTree 类的示例代码:
import bisect
class LSMTree:
def __init__(self):
self.memtable = {}
self.sstable = []
# 写操作
def put(self, key, value):
self.memtable[key] = value
if len(self.memtable) >= THRESHOLD:
self.flush()
if len(self.sstable) > LEVEL_THRESHOLD:
self.merge()
# 将内存表中的数据写入磁盘,形成新的SSTable文件
def flush(self):
keys = sorted(self.memtable.keys())
values = [self.memtable[key] for key in keys]
sstable = SSTable(keys, values)
self.sstable.append(sstable)
self.memtable.clear()
# 合并操作:将多个SSTable合并成一个更大的SSTable,并按照键的顺序排序
def merge(self):
new_sstable = []
# 将所有SSTable的键值对合并成一个列表
entries = []
for sstable in self.sstable:
entries.extend(zip(sstable.keys, sstable.values))
# 对键值对列表按照键排序
entries.sort(key=lambda x: x[0])
# 按照指定大小拆分键值对列表,并生成新的SSTable对象
i = 0
while i < len(entries):
keys, values = zip(*entries[i:i+SSTABLE_SIZE])
new_sstable.append(SSTable(list(keys), list(values)))
i += SSTABLE_SIZE
# 更新SSTable列表
self.sstable = new_sstable
# 读操作
def get(self, key):
# 从内存表中查询
if key in self.memtable:
return self.memtable[key]
# 从SSTable中查询(从后往前遍历,直到找到为止)
for sstable in reversed(self.sstable):
result = sstable.get(key)
if result is not None:
return result
return None
class SSTable:
def __init__(self, keys, values):
self.keys = keys
self.values = values
# 使用二分查找从SSTable中查询指定键的值
def get(self, key):
index = bisect.bisect_left(self.keys, key)
if index < len(self.keys) and self.keys[index] == key:
return self.values[index]
return None
在以上示例代码中,我们在 put 方法中添加了一个检查,当 SSTable 的数量超过阈值 LEVEL_THRESHOLD 时,将执行合并操作。
合并操作会将所有 SSTable 的键值对合并成一个更大的 SSTable,并按照键的顺序进行排序。
然后,我们根据指定的大小拆分键值对列表,并生成新的 SSTable 对象。最后,更新 SSTable 列表为新生成的 SSTable 列表。
需要注意的是,在实际实现中可能需要处理一些并发控制和数据一致性的问题,例如在合并操作期间,可能需要对读写操作进行锁定以防止数据被修改。
此外,还可以根据具体需求对合并操作进行优化和扩展,比如使用更复杂的合并策略来减少 IO 操作和提高查询效率。
再给点提示:现在需要加入事务支持,请问如何改造上面的 LSMTree 类代码
要在上面的 LSMTree 类代码中加入事务支持,可以进行以下改造:
- 添加一个新的类 Transaction,用于表示事务。Transaction 类可以包含以下属性:
- 一个标识符用于唯一表示该事务
- 一个字典用于存储在事务中插入或更新的键值对
- 一个列表用于存储在事务中删除的键
在 LSMTree 类中添加一个字典属性来存储所有进行中的事务。该字典的键是事务的标识符,值是对应的 Transaction 对象。
在 LSMTree 类中添加以下方法来支持事务操作:
- begin_transaction(): 开始一个新的事务。
- 生成一个新的事务标识符。
- 创建一个新的 Transaction 对象,并将其添加到进行中的事务字典中。
- commit_transaction(transaction_id): 提交一个事务。
- 根据提供的事务标识符获取对应的 Transaction 对象。
- 将该事务中插入或更新的键值对依次写入 LSM 树中。
- 将该事务中删除的键依次从 LSM 树中删除。
- 从进行中的事务字典中移除该事务。
- abort_transaction(transaction_id): 中止一个事务。
- 根据提供的事务标识符获取对应的 Transaction 对象。
- 清空该事务中插入或更新的键值对。
- 从进行中的事务字典中移除该事务。
- 修改 LSMTree 类的相应方法,以支持事务操作:
- put(key, value): 将键值对插入到当前事务的 Transaction 对象中。如果没有事务,则直接将其插入到 LSM 树中。
- delete(key): 将键添加到当前事务的 Transaction 对象的删除列表中。如果没有事务,则直接将其从 LSM 树中删除。
- get(key): 首先检查进行中的事务字典中是否有对应的事务,如果有,则返回该事务中的键值对。如果没有,则从 LSM 树中检索。
通过以上改造,LSMTree 类就具备了事务支持能力。在进行事务操作时,可以通过 begin_transaction()方法开始一个新的事务,然后在事务中使用 put()和 delete()方法进行插入、更新和删除操作,最后使用 commit_transaction()方法提交事务。或者使用 abort_transaction()方法中止事务。
一个字:强!请将完整代码给出:
下面是根据以上改造说明完成的 LSMTree 类的代码:
import uuid
class LSMTree:
def __init__(self):
self.memtable = {} # 内存表(字典),用于暂时存储插入或更新的键值对
self.disktable = [] # 磁盘表(列表),用于存储已经稳定的键值对
self.transactions = {} # 进行中的事务字典,用于存储所有进行中的事务
def begin_transaction(self):
transaction_id = str(uuid.uuid4())
transaction = Transaction(transaction_id)
self.transactions[transaction_id] = transaction
def commit_transaction(self, transaction_id):
transaction = self.transactions.get(transaction_id)
if transaction:
# 将事务中插入或更新的键值对写入LSM树
for key, value in transaction.data.items():
self.memtable[key] = value
# 从LSM树中删除事务中删除的键
for key in transaction.deleted_keys:
self.memtable.pop(key, None)
# 从进行中的事务字典中移除该事务
del self.transactions[transaction_id]
def abort_transaction(self, transaction_id):
transaction = self.transactions.get(transaction_id)
if transaction:
# 清空事务中插入或更新的键值对
transaction.data.clear()
# 从进行中的事务字典中移除该事务
del self.transactions[transaction_id]
def put(self, key, value):
current_transaction = self.transactions.get(self.current_transaction_id)
if current_transaction:
# 如果当前存在事务,则将键值对插入到事务的数据字典中
current_transaction.data[key] = value
else:
# 如果没有事务,则直接插入到LSM树中
self.memtable[key] = value
def delete(self, key):
current_transaction = self.transactions.get(self.current_transaction_id)
if current_transaction:
# 如果当前存在事务,则将键添加到事务的删除列表中
current_transaction.deleted_keys.append(key)
else:
# 如果没有事务,则直接从LSM树中删除键
self.memtable.pop(key, None)
def get(self, key):
current_transaction = self.transactions.get(self.current_transaction_id)
if current_transaction:
# 如果当前存在事务,则首先在事务中检索键值对
value = current_transaction.data.get(key)
if value is not None:
return value
# 在LSM树中检索键值对
value = self.memtable.get(key)
if value is not None:
return value
for disktable in self.disktable:
if key in disktable:
return disktable[key]
return None
class Transaction:
def __init__(self, transaction_id):
self.transaction_id = transaction_id
self.data = {} # 用于存储插入或更新的键值对
self.deleted_keys = [] # 用于存储删除的键
以上是加入事务支持的 LSMTree 类的完整代码。
通过使用该类,可以创建一个 LSM 树,并使用 begin_transaction()方法开始一个新的事务,在事务中使用 put()和 delete()方法进行插入、更新和删除操作,最后使用 commit_transaction()方法提交事务。或者使用 abort_transaction()方法中止事务。
在进行读取操作时,get()方法会首先在进行中的事务中检索键值对,如果没有找到,则继续在 LSM 树中检索。
测试
学习从未如此轻松!将 ChatGPT 给出的LSMTree稍加修饰,我们测试看看效果:
# Test code
if __name__ == "__main__":
lsm_tree = LSMTree()
transaction_id = lsm_tree.begin_transaction()
lsm_tree.put("a", "1", transaction_id)
lsm_tree.put("b", "2", transaction_id)
lsm_tree.put("c", "3", transaction_id)
assert lsm_tree.get("a") == None
assert lsm_tree.get("b") == None
assert lsm_tree.get("c") == None
print(lsm_tree.get("a", transaction_id))
print(lsm_tree.get("b", transaction_id))
print(lsm_tree.get("c", transaction_id))
lsm_tree.commit_transaction(transaction_id)
lsm_tree.put("d", "4")
lsm_tree.put("e", "5")
lsm_tree.put("f", "6")
lsm_tree.put("g", "7")
lsm_tree.put("h", "8")
lsm_tree.put("i", "9")
assert len(lsm_tree.memtable) == 9
lsm_tree.put("j", "10")
lsm_tree.put("k", "11")
assert len(lsm_tree.memtable) == 1
assert len(lsm_tree.sstable) == 1
assert lsm_tree.get("a") == "1"
lsm_tree.put("l", "12")
lsm_tree.put("m", "13")
lsm_tree.put("n", "14")
lsm_tree.put("o", "15")
lsm_tree.put("p", "16")
lsm_tree.put("q", "17")
lsm_tree.put("r", "18")
lsm_tree.put("s", "19")
lsm_tree.put("t", "20")
lsm_tree.put("u", "21")
assert len(lsm_tree.memtable) == 1
lsm_tree.put("v", "22")
lsm_tree.put("w", "23")
lsm_tree.put("x", "24")
lsm_tree.put("y", "25")
lsm_tree.put("z", "26")
lsm_tree.put("aa", "27")
lsm_tree.put("bb", "28")
lsm_tree.put("cc", "29")
lsm_tree.put("dd", "30")
lsm_tree.put("ee", "31")
assert len(lsm_tree.memtable) == 1
assert lsm_tree.get("a") == "1"
assert lsm_tree.get("aa") == "27"
# Output
# 1
# 2
# 3
测试通过,基本覆盖了flush和merge等全部操作,虽然无法直接用于生产,但对于了解原理和get hands dirty来说,已经足够了。
完整代码见:LSMTree.py,基本些许更改就能 work 了。
